Even and odd signals

Even Signal

A signal is said to be even if it satisfies the following condition;

x(−t)=x(t)$$x(-t)=x(t)$$

Time reversal of the signal does not imply any change on amplitude here. For example, consider the triangular wave shown below.

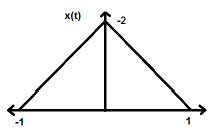
The triangular signal is an even signal. Since, it is symmetrical about Y-axis. We can say it is mirror image about Y-axis.

Consider another signal as shown in the figure below.

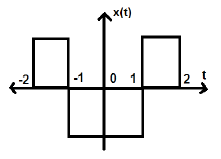
We can see that the above signal is even as it is symmetrical about Y-axis.

Odd Signal

A signal is said to be odd, if it satisfies the following condition

x(−t)=−x(t)$$x(-t)=-x(t)$$

Here, both the time reversal and amplitude change takes place simultaneously.

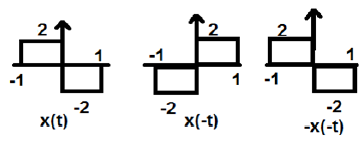
In the figure above, we can see a step signal x(t). To test whether it is an odd signal or not, first we do the time reversal i.e. x(-t) and the result is as shown in the figure. Then we reverse the amplitude of the resultant signal i.e. –x(-t) and we get the result as shown in figure.

If we compare the first and the third waveform, we can see that they are same, i.e. x(t)= -x(-t), which satisfies our criteria. Therefore, the above signal is an Odd signal.

Some important results related to even and odd signals are given below.

• Even × Even = Even
• Odd × Odd = Even
• Even × Odd = Odd
• Even ± Even = Even
• Odd ± Odd = Odd
• Even ± Odd = Neither even nor odd

Representation of any signal into even or odd form

Some signals cannot be directly classified into even or odd type. These are represented as a combination of both even and odd signal.

x(t)→xe(t)+x0(t)$$x(t)\to x_e(t)+x_0(t)$$

Where x_e(t) represents the even signal and x_o(t) represents the odd signal

xe(t)=[x(t)+x(−t)]2$$x_e(t)=\frac{[x(t)+x(-t)]}{2}$$

And

x0(t)=[x(t)−x(−t)]2$$x_0(t)=\frac{[x(t)-x(-t)]}{2}$$

Example

Find the even and odd parts of the signal x(n)=t+t2+t3$x(n)=t+t^2+t^3$

Solution − From reversing x(n), we get

x(−n)=−t+t2−t3$$x(-n)=-t+t^2-t^3$$

Now, according to formula, the even part

xe(t)=x(t)+x(−t)2$$x_e(t)=\frac{x(t)+x(-t)}{2}$$

=[(t+t2+t3)+(−t+t2−t3)]2$$=\frac{[(t+t^2+t^3)+(-t+t^2-t^3)]}{2}$$

=t2$$=t^2$$

Similarly, according to formula the odd part is

x0(t)=[x(t)−x(−t)]2$$x_0(t)=\frac{[x(t)-x(-t)]}{2}$$

=[(t+t2+t3)−(−t+t2−t3)]2$$=\frac{[(t+t^2+t^3)-(-t+t^2-t^3)]}{2}$$

=t+t3