Amplitude shifting

Amplitude shifting means shifting of signal in the amplitude domain (around X-axis). Mathematically, it can be represented as −

x(t)→x(t)+K$$x(t)\to x(t)+K$$

This K value may be positive or negative. Accordingly, we have two types of amplitude shifting which are subsequently discussed below.

Case 1 (K > 0)

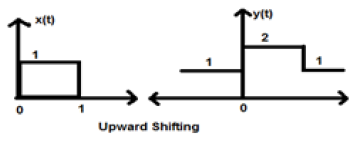
When K is greater than zero, the shifting of signal takes place towards up in the x-axis. Therefore, this type of shifting is known as upward shifting.

Example

Let us consider a signal x(t) which is given as;

x=⎧⎩⎨0,1,0,t<00≤t≤2t>0$$x=\{\begin{array}{ll}0,& t<0\\ 1,& 0\le t\le 2\\ 0,& t>0\end{array}$$

Let we have taken K=+1 so new signal can be written as −

y(t)→x(t)+1$y(t)\to x(t)+1$ So, y(t) can finally be written as;

x(t)=⎧⎩⎨1,2,1,t<00≤t≤2t>0$$x(t)=\{\begin{array}{ll}1,& t<0\\ 2,& 0\le t\le 2\\ 1,& t>0\end{array}$$

Case 2 (K < 0)

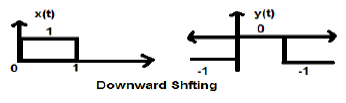
When K is less than zero shifting of signal takes place towards downward in the X- axis. Therefore, it is called downward shifting of the signal.

Example

Let us consider a signal x(t) which is given as;

x(t)=⎧⎩⎨0,1,0,t<00≤t≤2t>0$$x(t)=\{\begin{array}{ll}0,& t<0\\ 1,& 0\le t\le 2\\ 0,& t>0\end{array}$$

Let we have taken K = -1 so new signal can be written as;

y(t)→x(t)−1$y(t)\to x(t)-1$ So, y(t) can finally be written as;

y(t)=⎧⎩⎨−1,0,−1,t<00≤t≤2t>0$$y(t)=\{\begin{array}{ll}-1,& t<0\\ 0,& 0\le t\le 2\\ -1,& t>0\end{array}$$