Energy and power signals

A signal is said to be an Energy signal, if and only if, the total energy contained is finite and nonzero (0<E<∞). Therefore, for any energy type signal, the total normalized signal is finite and non-zero.

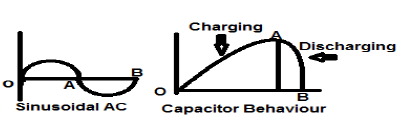
A sinusoidal AC current signal is a perfect example of Energy type signal because it is in positive half cycle in one case and then is negative in the next half cycle. Therefore, its average power becomes zero.

A lossless capacitor is also a perfect example of Energy type signal because when it is connected to a source it charges up to its optimum level and when the source is removed, it dissipates that equal amount of energy through a load and makes its average power to zero.

For any finite signal x(t) the energy can be symbolized as E and is written as;

E=∫+∞−∞x2(t)dt$$E={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{x}^2(t)dt$$

Spectral density of energy type signals gives the amount of energy distributed at various frequency levels.

Power type Signals

A signal is said to be power type signal, if and only if, normalized average power is finite and non-zero i.e. (0<p<∞). For power type signal, normalized average power is finite and non-zero. Almost all the periodic signals are power signals and their average power is finite and non-zero.

In mathematical form, the power of a signal x(t) can be written as;

P=limT→∞1/T∫+T/2−T/2x2(t)dt$$P=\underset{T\to \mathrm{\infty }}{lim}1/T{\int }_{-T/2}^{+T/2}{x}^2(t)dt$$

Difference between Energy and Power Signals

The following table summarizes the differences of Energy and Power Signals.

Power signal	Energy Signal
Practical periodic signals are power signals.	Non-periodic signals are energy signals.
Here, Normalized average power is finite and non-zero.	Here, total normalized energy is finite and non-zero.
Mathematically, P=limT→∞1/T∫+T/2−T/2x2(t)dt$$P=\underset{T\to \mathrm{\infty }}{lim}1/T{\int }_{-T/2}^{+T/2}{x}^2(t)dt$$	Mathematically, E=∫+∞−∞x2(t)dt$$E={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{x}^2(t)dt$$
Existence of these signals is infinite over time.	These signals exist for limited period of time.
Energy of power signal is infinite over infinite time.	Power of the energy signal is zero over infinite time.

Solved Examples

Example 1 − Find the Power of a signal z(t)=2cos(3Πt+30o)+4sin(3Π+30o)$z(t)=2\cos (3\mathrm{\Pi }t+{30}^o)+4\sin (3\mathrm{\Pi }+{30}^o)$

Solution − The above two signals are orthogonal to each other because their frequency terms are identical to each other also they have same phase difference. So, total power will be the summation of individual powers.

Let z(t)=x(t)+y(t)$z(t)=x(t)+y(t)$

Where x(t)=2cos(3Πt+30o)$x(t)=2\cos (3\mathrm{\Pi }t+{30}^o)$ and y(t)=4sin(3Π+30o)$y(t)=4\sin (3\mathrm{\Pi }+{30}^o)$

Power of x(t)=222=2$x(t)=\frac{2^2}{2}=2$

Power of y(t)=422=8$y(t)=\frac{4^2}{2}=8$

Therefore, P(z)=p(x)+p(y)=2+8=10$P(z)=p(x)+p(y)=2+8=10$…Ans.

Example 2 − Test whether the signal given x(t)=t2+jsint$x(t)=t^2+j\sin t$ is conjugate or not?

Solution − Here, the real part being t² is even and odd part (imaginary) being sint$\sin t$ is odd. So the above signal is Conjugate signal.

Example 3 − Verify whether X(t)=sinωt$X(t)=\sin \omega t$ is an odd signal or an even signal.

Solution − Given X(t)=sinωt$X(t)=\sin \omega t$

By time reversal, we will get sin(−ωt)$\sin (-\omega t)$

But we know that sin(−ϕ)=−sinϕ$\sin (-\varphi )=-\sin \varphi$.

Therefore,

sin(−ωt)=−sinωt$$\sin (-\omega t)=-\sin \omega t$$

This is satisfying the condition for a signal to be odd. Therefore, sinωt$\sin \omega t$ is an odd signal.