The convolution of two signals in the time domain is equivalent to the multiplication of their representation in frequency domain. Mathematically, we can write the convolution of two signals as
Steps for convolution
- Take signal x1(t) and put t = p there so that it will be x1(p).
- Take the signal x2(t) and do the step 1 and make it x2(p).
- Make the folding of the signal i.e. x2(-p).
- Do the time shifting of the above signal x2[-(p-t)]
- Then do the multiplication of both the signals. i.e.
Example
Let us do the convolution of a step signal u(t) with its own kind.
Now this t can be greater than or less than zero, which are shown in below figures
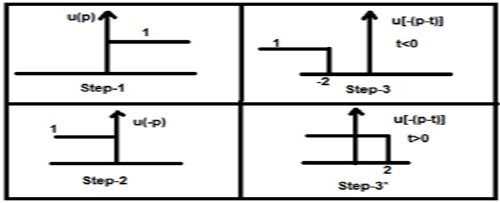
So, with the above case, the result arises with following possibilities
Properties of Convolution
Commutative
It states that order of convolution does not matter, which can be shown mathematically as
Associative
It states that order of convolution involving three signals, can be anything. Mathematically, it can be shown as;
Distributive
Two signals can be added first, and then their convolution can be made to the third signal. This is equivalent to convolution of two signals individually with the third signal and added finally. Mathematically, this can be written as;
Area
If a signal is the result of convolution of two signals then the area of the signal is the multiplication of those individual signals. Mathematically this can be written
If
Then, Area of y(t) = Area of x1(t) X Area of x2(t)
Scaling
If two signals are scaled to some unknown constant “a” and convolution is done then resultant signal will also be convoluted to same constant “a” and will be divided by that quantity as shown below.
If,
Then,
Delay
Suppose a signal y(t) is a result from the convolution of two signals x1(t) and x2(t). If the two signals are delayed by time t1 and t2 respectively, then the resultant signal y(t) will be delayed by (t1+t2). Mathematically, it can be written as −
If,
Then,